On the error control side, most work has focused on providing end-to-end reliability based on retransmissions [4, 5, 6] or hybrid schemes employing forward error correction (FEC) and retransmissions [7,8]. Because the cost of retransmissions in a multicast setting is high, such schemes are often justified only for low bandwidth applications that require reliability, such as the shared white-board in the MBONE tools. Retransmissions may also be inapplicable for real-time applications, especially when round trip time is long. In contrast, pure FEC based schemes are simpler, but can be wasteful as redundancy packets are transmitted to all receivers regardless of whether they are needed or not.
In this work, we will investigate the application of hierarchical FEC as an error control method for scalable video multicasting. By hierarchical FEC, we mean the production of embedded FEC or redundancy streams, each of which belongs to a different multicast group. In such a way, subscribing to more groups corresponds to higher level of protection. There are two advantages to using hierarchical FEC. First, each receiver can independently adjust the desired level of protection based on past reception statistics and the application's delay tolerance. This receiver-driven approach to FEC is more flexible than most existing FEC schemes for multicast where the source determines a set of redundancy packets which are then multicast to every recipient [8]. Second, each receiver will subscribe to only as many redundancy layers as necessary, reducing overall bandwidth utilization. Thus, the hierarchical nature of the FEC layers ensures minimum network utilization through sharing of common streams. An effective means to combat burstiness in packet losses is suggested in [9] where redundancy packets are transmitted at a later time than the actual data packets. Following [9], we delay the transmission of FEC layers to relieve the effects of bursty losses. The additional latency associated with the FEC layers creates a trade-off between higher levels of protection and increased latency, and also as a disincentive for receivers to unnecessarily use FEC.
The use of scalable video has three implications. First, it is possible to achieve flow control by adjusting the number of data layers based on the observed channel characteristics. Second, it is possible to drop data layers to make room for FEC layers so as not to increase overall transmission rate. Third, it is possible to strategically provide FEC only to the most important data layer so as to reduce the amount of FEC traffic. The optimal division of the available bandwidth between data and FEC depends on the error resilience of the scalable video source. Since less error-resilient compression schemes suffer higher penalty when packets are lost, they tend to allocate larger portions of the available bandwidth for FEC. This generally causes the quality of the received video to be lower. As a result, it is desirable to have error resilience even when FEC is used for error control. In this paper, we will evaluate our framework using a scalable and error resilient compression scheme that we have developed for Internet transmissions [18,19,20].
The remaining of the paper is organised as follows. An overview of our proposed system architecture is described in Section 2. The selection of error control code for implementing the hierarchical FEC is described in Section 3. We will describe our scalable video compression scheme and its application to the proposed hierarchical FEC framework in Section 4 and present experimental results in Section 5. Conclusion and future work are in Section 6.

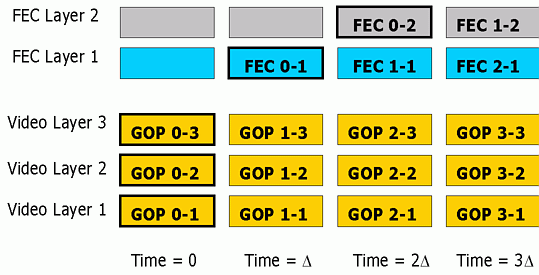
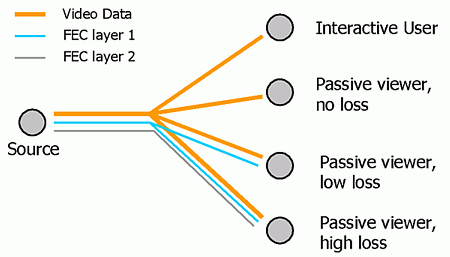
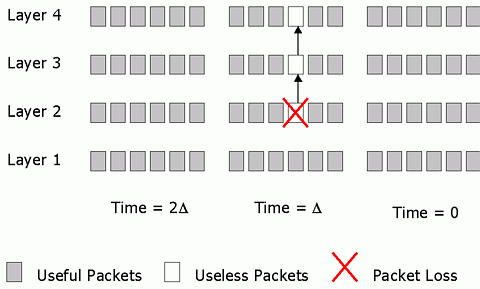
Addresses D1, D2, D3 are used to carry layered video data and addresses R1, R2 are used to carry redundancy packets. All layers of video data corresponding to the same group of pictures (GOP) that are compressed together are transmitted in the same time slot. As a result, users with stringent delay requirements can simply subscribe to D1, and possibly D2 and D3 depending on the bandwidth that is available to them. Users with higher tolerance of latency who are also experiencing packet losses can subscribe to addresses R1 and potentially R2 to obtain redundancy to repair lost packets at the cost of extra delay. The reason for spreading the redundancy layers for the same GOP across different time slots is to achieve interleaving, which is an effective means of combating bursty losses often experienced in the Internet [9]. Fig. 2 summarizes the behavior for different users. We see that FEC packets are only transmitted to branches that lead to subscribers requiring FEC, thereby reducing overall network load.
In order to determine the optimum distribution of FEC
packets across video layers, one can setup and solve an optimization problem
[18]. Instead, in the experiments reported
in this paper, we only apply FEC to the first layer of Video rather than
all layers. The approach is motivated by the fact
that (1) the first layer video is generally much more important than other
layers, and (2) it reduces the computation each receiver needs to decide
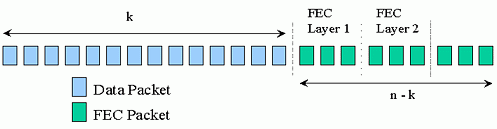
the number of FEC layers to subscribe to. The packets in the FEC
layers are generated by applying the FEC code described in Section
3 on the packet level. The sizes of the FEC layers determine
the granularity of available protection. Generally, providing many
small FEC layers improves the granularity of available protection levels
but incurs a higher networking overhead associated with maintaining the
larger number of multicast groups.
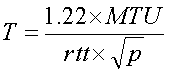 (1)
(1)Because the problem of rate control in a layered multicast setting is still an area of active research and that our proposed hierarchical FEC scheme does not depend on any specific rate control scheme, we adopt a simple rate control algorithm which is sufficient for the scale of experiments we are performing. Specifically, our rate control scheme is similar to [10] in that every receiver estimates the available bandwidth according to Equation 1 in an uncoordinated fashion. To avoid unnecessary reaction to network transients, the bandwidth calculation is performed relatively infrequently, with a period of 50 seconds. The packet loss rate p is measured over the whole period, and over all data and FEC layers while rtt is updated only once every 5 seconds to reduce the load on the source. Clearly, it is possible to augment our rate control approach by adding synchonization mechanisms as in [12].
Given a dynamic bandwidth constraint obtained by periodically applying Equation 1, the receiver then decides on the optimal number of data versus FEC layers to subscribe. The partition of bandwidth between data and FEC depends on the characteristics of the scalable video compression method used and is described in Section 4.2.
The successive refinement property of Reed-Solomon codes has long been exploited in data communications to provide incremental redundancy. For example, in the scheme of [15], a sender will continually transmit parity packets until a receiver has enough parity packet to recover all lost data packets. More recently, the dual code of Reed-Solomon code, which is also MDS, has been used to reduce the average transmission time of data in a large reliable data multicast setting [16].
Following [16], we select the dual code of the Reed-Solomon code as the MDS code for generating FEC packets. The dual code has no theoretical advantage over Reed-Solomon code and is chosen primarily because of the availability of existing software implementations [17].
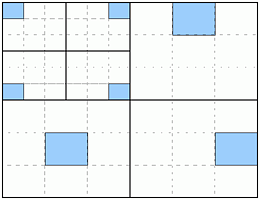
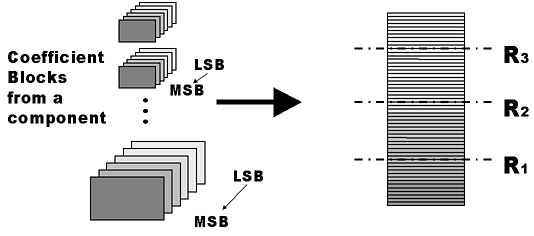
Each component is then compressed independently as follows.
Each coefficient block is split into bit-planes. Each bit-plane is compressed
using hierarchical block coding of [19] to produce
a small codeword which provides fine granularity for layered packetization.
Packetization is carried out so that the bit-plane offering the best rate-distortion
trade-off is packed first. The scheme is illustrated in Fig.
6.
Assume constant packet sizes. When d layers of data are subscribed by a receiver, the expected distortion is given by:
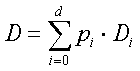 (2)
(2)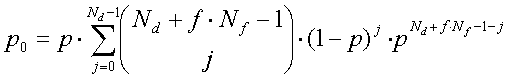
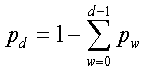
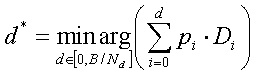
We perform two experiments. In the first experiment, both receivers have stringent real-time requirements so that no FEC layers will be subscribed to. In the second experiment, which is run immediately after the first one, receivers are non-interactive and when loss rates are non-trivial, they may sacrifice some data layers to yield bandwidth to FEC layers.
In our experiments, the link from Berkeley to Georgia Tech is never congested and no packet losses are observed. As a result, the receiver at Georgia Tech is subscribing at the maximum number of 4 data layers and without any FEC layers in both experiments. The link from Berkeley to ISI however, has an average packet loss rate of over 18% and given a rtt of about 28 ms, Equation 1 results in an average throughput of 400 kbps. In the first experiment, all of the 400 kbps is allocated to data whereas in the second experiment, 200 kbps is allocated to data and the other 200 kbps to FEC. The partition of bandwidth between FEC and data is determined by the measured packet loss rate in such a way that the expected distortion is minimized, as described in Section 4.2. The rate-distortion characteristics of the video is precomputed at the source and released to the receivers before the experiment.
Fig. 7 shows the packet loss rates experienced at the different data layers in the two experiments for the connection from Berkeley to ISI. It is observed that the actual observed packet loss rates do not change significantly between the two experiments and that the packet loss rate across layers is more or less constant.
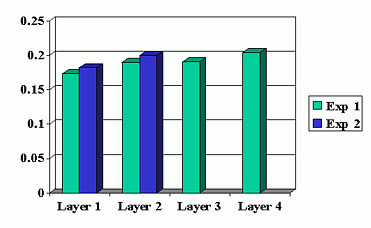
Fig. 8 shows the the fraction of packets received per GOP for experiment 2 for the Berkeley to ISI connection. We observe that when measured over intervals of 1/3 second, packet losses show much burstiness, which necessitates the delay in sending the FEC layers.
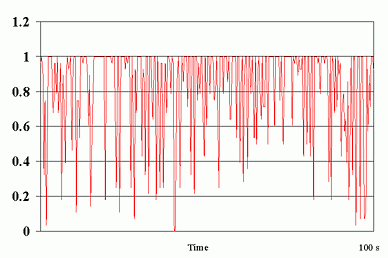
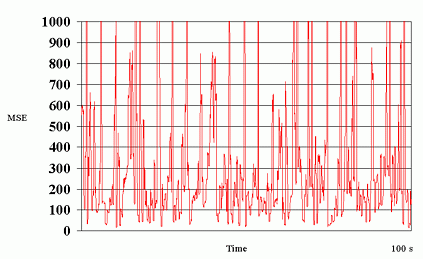
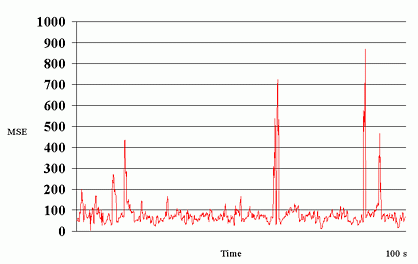
There are several issues that need to be addressed further. First, the current approach to determine the number of FEC layers are based on minimization of expected distortion assuming independent packet losses. More meaningful metrics that yield visually pleasing rather than minimum mean squared error video are desired. Second, the current approach to flow control is completely decentralized. Even though the receivers do not actively probe for bandwidth, the adding and dropping of layers are uncoordinated. It is interesting to investigate whether synchronization techniques as proposed in [12,13] are necessary for the network to achieve stability. Third, the current transport protocol is plain UDP. The additional incorporation of RTP would provide a standardized framework for the measurements of quantities such as round-trip time and delay jitter.
[2] N.Shacham. Multipoint Communication by Hierarchically Encoded Data Proc. Infocomm, pp 2107-2114, May 1992.
[3] B.Vickers, C.Albuquerque and T.Suda. Adaptive Multicast of Multi-layered Video: Rate-based and Credit-based Approaches. Proc. Infocomm, pp 1073-1083, March 1998.
[4] S.Floyd, V.Jacobson, C.Liu, S.McCanne and L.Zhang. A Reliable Multicast Framework for Light-weight Sessions and Application Level Framing. IEEE Trans. Networking, Vol. 5, No. 6, pp 784-803, December 1997.
[5] X.Xu, A.Myers, H.Zhang and R.Yavatkar. Resilient Multicast Support for Continuous Media Applications. Proc. NOSSDAV '97, pp 183-194, May 1997.
[6] X.Li, S.Paul, P.Pancha and M.Ammar, Layered Video Multicast with Retransmissions (LVMR): Evaluation of Error Recovery Schemes. Proc. NOSSDAV '97. pp 161-172, May 1997.
[7] S.Pejhan and M.Schwartz. Error Control using Retransmission Schemes in Multicast Transport Protocols for Real-time Media, IEEE Trans. Networking, Vol. 4, No. 3, pp 413-427, June 1996.
[8] J.Nonnenmacher, E.Biersack and D.Towsley. Parity-based Loss Recovery for Reliable Multicast Transmission. IEEE/ACM Trans. Networking, Vol. 6, No. 4, pp 349-361, August 1998.
[9] J.Bolot and A.Vega-Garcia. The case for FEC based Error Control for Packet Audio in the Internet., ACM Multimedia Sys.1997.
[10] T.Turletti, S.Parisis and J.Bolot. Experiments with a Layered Transmission Scheme over the Internet. INRIA Technical Report. http://www.inria.fr/RRRT/RR-3296.html
[11] M.Mathis, J.Semke, J.Mahdavi and T.Ott. The Macroscopic Behavior of the TCP Congestive Avoidance Algorithm. CCR, Vol. 27, No. 3, July 1997.
[12] L.Vicisano, L.Rizzo and J.Crowcroft. TCP-like Congestion Control for Layered Multicast Data Transfer. Proc. InfoComm 98, Vol. 3, pp 996-1003, March 1998.
[13] X.Li, S.Paul and M.Ammar. Layered Video Multicast with Retransmissions (LVMR): Evaluation of Hierarchical Rate Control. Proc. Infocomm '98. pp 1062-1072, March 1998.
[14] S.Wicker. Error Control Systems for Digital Communication and Storage. Prentice-Hall, 1995.
[15] D.Mandelbaum. An Adaptive-Feedback Coding Scheme using Incremental Redundancy. IEEE Trans. Info. Theory, Vol. IT-20, No. 3, pp 388-389, May 1974.
[16] L.Rizzo and V.Visano. A Reliable Multicast Data Distribution Protocol based on Software FEC Techniques. Proc. 4th IEEE Workshop Arch. and Implementation of High Perf. Comm. Sys. (HPCS 97), 1997.
[17] L.Rizzo. Effective Erasure Codes for Reliable Computer Communication Protocols. CCR, Vol. 27, No. 2, pp 24-36, April 1997.
[18] W.Tan and A.Zakhor. Real-time Internet Video using Error Resilient Scalable Compression and TCP-friendly Transport Protocol. To appear in IEEE Trans. Multimedia.
[19] W.Tan, E.Chang and A.Zakhor. Real Time Software Implementation of Scalable Video Codec. Proc. ICIP, Vol. 1, pp 17-20, September 1996.
[20] W.Tan and A.Zakhor. Internet Video using Error-resilient Scalable Video Compression and Cooperative Transport Protocol. Proc. ICIP 98, Vol. 3, pp 458-462, October 1998.
[21] K.Patel, B.Smith and L.Rowe.
Performance of a Software MPEG Video Decoder. Proc. of ACM Multimedia
'93, pp 75-82, 1993.
[22] D.Taubman and A.Zakhor. Multirate
3-D Subband Coding of Video. IEEE Trans. Image Proc., Vol. 3, No.
5, pp 572-588, September 1994.